우리는 원하는 값을 얻기 위해서 탐색을 합니다. 널리 쓰이는 탐색 중 하나인 이진 탐색은 탐색량을 줄이기 적합한 탐색 방법입니다.
이진 탐색은 정렬된 배열에서만 사용 가능한데 배열은 중간 삽입, 삭제가 느리고 임의 접근이 불가능 하기 때문에 정렬된 연결리스트로는 접근을 하지 못한다는 단점이 있습니다.
따라서 이진 탐색에서 더 나아간 이진 탐색 트리를 사용하면 중간 삽입, 삭제가 가능하고 연결리스트 또한 접근이 가능합니다.
[이진 탐색 트리]

이진 탐색 트리는 조건을 4가지 가지고 있습니다.
조건
1. 각 노드는 유일한 키를 가지고 있다.
2. 왼쪽 서브 트리에 있는 키들은 모두 루트 노드의 키보다 작다.
3. 오른쪽 서브 트리에 있는 키들은 모두 루트노드의 키보다 크다.
4. 왼쪽 서브 트리와 오른쪽 서브 트리도 이진 탐색 트리다.
[이진 탐색 트리 추가, 탐색, 삭제]
1. 추가 (insert)

처음 들어온 20은 root가 됩니다.
2번째로 들어온 25는 20보다 크기 때문에 20의 오른쪽 자식이 됩니다.
3번째로 들어온 14는 20보다 작기 때문에 20의 왼쪽 자식이 됩니다.
4번째로 들어온 30은 20보다 크고 25보다 크기 때문에 25의 오른쪽 자식이 됩니다.
5번째로 들어온 23은 20보다 크고 25보다 작기 때문에 25의 왼쪽 자식이 됩니다.
이런식으로 이진 탐색 트리의 추가가 이루어집니다.
2. 탐색
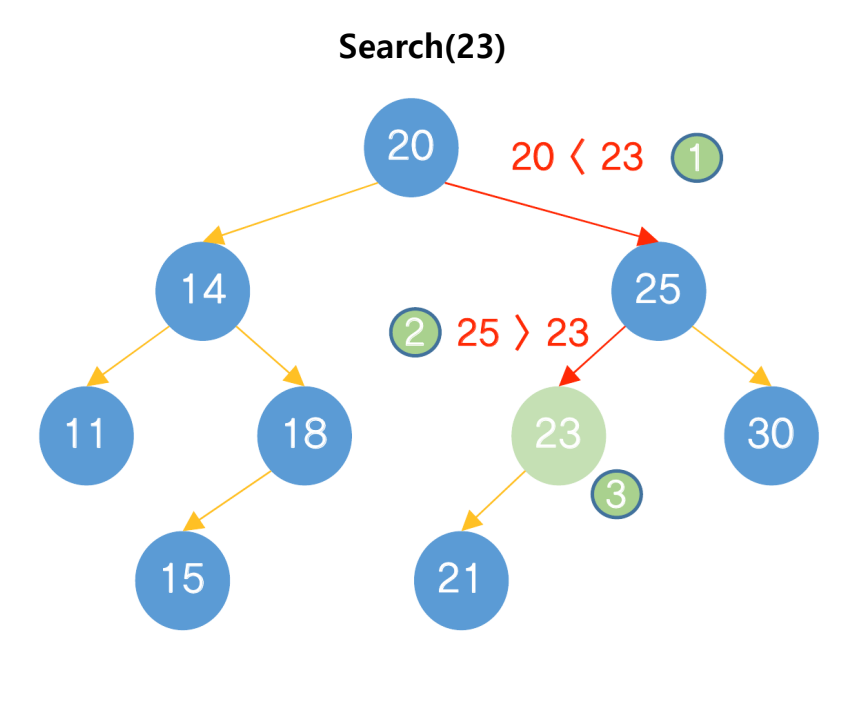
지금 찾으려는 값은 23입니다.
23은 20보다 크기 때문에 오른쪽으로 탐색 범위를 좁힙니다.
23은 25보다 작기 때문에 왼쪽으로 탐색 범위를 좁힙니다.
23을 찾아 탐색을 종료합니다.
3. 삭제
- 단노드를 삭제할 경우

단노드는 자식이 없는 노드이기 때문에 그냥 삭제해주면 됩니다.
- 자식이 1개인 노드를 삭제하는 경우

18을 삭제할 때 자식이 15 밖에 없기 때문에 18을 삭제한 뒤에 15를 18의 자리로 넣어주면 됩니다.
- 자식이 2개인 노드를 삭제하는 경우

자식이 2개인 노드를 삭제하는 방법은 2가지가 있습니다.
1. 왼쪽 서브 노드의 가장 오른쪽에 있는 노드를 삭제한 노드 자리에 넣는다.
2. 오른쪽 서브 노드의 가장 왼쪽에 있는 노드를 삭제한 노드 자리에 넣는다.
2가지 방법이 존재하는 이유는 2가지 방법에서 찾은 노드가 삭제할 노드와 가장 값이 가까운 노드이기 때문입니다.
ex) 14를 삭제할 때 1번 방법을 사용한 경우 14자리에 넣어줄 노드는 11
14를 삭제할 때 2번 방법을 사용한 경우 14자리에 넣어줄 노드는 15
위 그림은 2번 방법을 사용하여 노드를 삭제한 경우입니다.
이렇게 이진 탐색 트리에 대해서 알아보았습니다.
'C++ 자료구조' 카테고리의 다른 글
| [c++] 다익스트라 알고리즘 | 최단 경로 (2) | 2024.10.09 |
|---|---|
| [c++] 그래프 구조 (DFS, BFS 탐색) (0) | 2024.09.03 |
| [c++] 트리(tree) (0) | 2024.08.12 |
| [c++] map과 set (0) | 2024.06.11 |
| [탐색] 순차 탐색, 이진 탐색 (0) | 2024.06.10 |



